ISO 11146 Beam Size Definitions¶

Scott Prahl

Mar 2021

A laser beam will usually consist of a superposition of several modes. A single mode beam radius is easily described by \(1/e^2\) points. This, of course, fails for any beam shape other than Gaussian. ISO 11146 is intended to provide a simple, consistent way of describing the width of a beam.

This notebook summarizes the mathematical definitions.

If laserbeamsize is not installed, uncomment the following cell (i.e., delete the initial #) and execute it with shift-enter. Afterwards, you may need to restart the kernel/runtime before the module will import successfully.

[1]:

#!pip install --user laserbeamsize

[2]:

import numpy as np
import matplotlib.pyplot as plt

try:
    import laserbeamsize as lbs

except ModuleNotFoundError:
    print('laserbeamsize is not installed. To install, uncomment and run the cell above.')
    print('Once installation is successful, rerun this cell again.')

[3]:

lbs.draw_beam_figure()

The total power \(P\) is obtained by integrating the irradiance \(E(x,y)\) over the entire beam

\[P = \int_{-\infty}^\infty \int_{-\infty}^\infty E(x,y)\,dxdy\]

Center of beam¶

The center of the beam can be found by

\[ \begin{align}\begin{aligned} x_c = {1\over P} \int_{-\infty}^\infty \int_{-\infty}^\infty x \cdot E(x,y)\,dxdy\\and\end{aligned}\end{align} \]

\[y_c = {1\over P} \int_{-\infty}^\infty \int_{-\infty}^\infty y \cdot E(x,y)\,dxdy\]

Variance¶

A useful parameter characterizing a general two-dimensional distribution \(E(x,y)\) is the variance in the \(x\) and \(y\) directions

\[ \begin{align}\begin{aligned} \sigma_x^2 = {1\over P} \int_{-\infty}^\infty \int_{-\infty}^\infty (x-x_c)^2 E(x,y)\,dxdy\\and\end{aligned}\end{align} \]

\[ \begin{align}\begin{aligned} \sigma_y^2 = {1\over P} \int_{-\infty}^\infty \int_{-\infty}^\infty (y-y_c)^2 E(x,y)\,dxdy\\and\end{aligned}\end{align} \]

\[\sigma_{xy}^2 = {1\over P} \int_{-\infty}^\infty \int_{-\infty}^\infty (x-x_c)(y-y_c) E(x,y)\,dxdy\]

In general, \(\sigma_x \ne \sigma_y\). For example, in semiconductor lasers the height and width of the emitting aperture differ. Such beams are called astigmatic.

Now, the quantities \(\sigma_x^2\) and \(\sigma_y^2\) will always be positive, but \(\sigma_{xy}^2\) can be negative, zero, or positive.

Beam Radius and \(D4\sigma\) or D4sigma¶

For a Gaussian distribution centered at (0,0) with \(1/e^2\) radius \(w\) we find

\[\sigma_x^2 = \frac{\int_{-\infty}^\infty \int_{-\infty}^\infty x^2 e^{-2(x^2+y^2)/w^2}\,dx\,dy}{ \int_{-\infty}^\infty \int_{-\infty}^\infty e^{-2(x^2+y^2)/w^2}\,dx\,dy} =\frac{w^2}{4}\]

This leads to the definition of the beam radius definition as adopted by ISO 11146,

\[w_x = 2\sigma_x \qquad w_y = 2\sigma_y\]

\(D4\sigma\) or D4sigma¶

The \(D4\sigma\) beam diameter is a simple rearrangement of the above equation in which it is noted that twice the radius or the beam diameter is equal to \(4\sigma\)

\[4\sigma_x = 2w_x\]

Relationship to FWHM¶

Sometimes it is the full width at half maximum (FWHM) value that is desired or known. In general, there is no direct relationship between the \(1/e^2\) radius \(w\) and the FWHM. However, in the special case of a Gaussian beam, there is.

\[w={ \mathrm {FWHM}\over \sqrt {2\ln 2}}\]

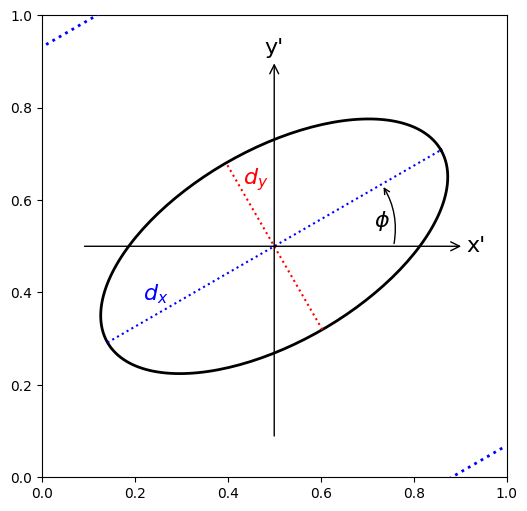
Major and minor axes of an elliptical beam¶

The \(x\)-axis diameter \(d_x=2w_x\) is given by

\[d_x = \sqrt{8(\sigma_x^2 + \sigma_y^2) + 8\operatorname{sign}(\sigma_x^2 -\sigma_y^2) \sqrt{(\sigma_x^2 -\sigma_y^2)^2+4\sigma_{xy}^4}}\]

and similarly \(d_y=2w_y\) is

\[d_y = \sqrt{8(\sigma_x^2 + \sigma_y^2) - 8\operatorname{sign}(\sigma_x^2 -\sigma_y^2) \sqrt{(\sigma_x^2 -\sigma_y^2)^2+4\sigma_{xy}^4}}\]

except if \(\sigma_x^2=\sigma_y^2\) in which case

\[d_x = \sqrt{8\sigma_x^2 + 8\sigma_y^2 + 16|\sigma_{xy}^2|}\]

and

\[d_y = \sqrt{8\sigma_x^2 + 8\sigma_y^2 - 16|\sigma_{xy}^2|}\]

The tilt angle of the ellipse \(\phi\)¶

This is measured as a positive angle counter-clockwise from the \(x\)-axis (see figure above).

\[\phi =\frac{1}{2}\arctan \frac{2\sigma_{xy}}{\sigma_x^2 -\sigma_y^2}\]

where we use np.arctan2(numerator,denominator) to avoid division by zero when \(\sigma_x^2=\sigma_y^2\)

Ellipticity and Eccentricity¶

The ellipticity \(e\) is

\[\varepsilon = \frac{\operatorname{min}(dx,dy)}{\operatorname{max}(dx,dy)}\]

and the eccentricity is

\[e = \sqrt{1-\varepsilon^2}\]